압축 기술
문제 1 : 차분 데이터의 Histogram
1. Grayscale Lenna에서 차분 값 Δ=X-(A+C)/2를 구한다.
2. Δ는 음수값이 나오므로 +128을 add 한다. 다음에 음수값은 0으로, 255를 초과하면 255로 clipping 해야 함.
3. 차분 데이터의 histogram을 출력한다.
정답 코드
#include <iostream>
// ...
int main(void)
{
// ...
int histogram[256];
for (int i = 0; i < 256; i++) // 초기화
histogram[i] = 0;
for (int i = 1; i < Height - 1; i++) {
for (int j = 1; j < Width - 1; j++) {
int sum = *(YBuf + i * Width + j) - ((*(YBuf + i * Width + j - 1) + *(YBuf + (i - 1) * Width + j)) / 2);
sum = sum + 128;
if (sum > 255) sum = 255;
if (sum < 0) sum = 0;
histogram[sum]++;
}
}
printf(" Y frequency \n");
for (int x = 0; x < 256; x++)
printf(" %d : %d \n", x, histogram[x]);
int total = 0;
for (int i = 0; i < 256; i++)
total += histogram[i];
printf(" total : %d \n", total);
// ...
}
결과
Y frequency
0 : 0
1 : 0
2 : 0
3 : 0
4 : 0
5 : 0
6 : 0
7 : 0
8 : 0
9 : 0
10 : 0
11 : 0
12 : 0
13 : 0
14 : 0
15 : 0
16 : 0
17 : 0
18 : 0
19 : 0
20 : 0
21 : 0
22 : 0
23 : 0
24 : 0
25 : 0
26 : 0
27 : 0
28 : 0
29 : 0
30 : 0
31 : 0
32 : 0
33 : 0
34 : 0
35 : 1
36 : 1
37 : 1
38 : 0
39 : 0
40 : 0
41 : 3
42 : 1
43 : 4
44 : 3
45 : 1
46 : 2
47 : 3
48 : 1
49 : 6
50 : 6
51 : 2
52 : 5
53 : 4
54 : 8
55 : 6
56 : 5
57 : 7
58 : 6
59 : 8
60 : 11
61 : 12
62 : 8
63 : 9
64 : 10
65 : 13
66 : 6
67 : 15
68 : 10
69 : 12
70 : 14
71 : 10
72 : 12
73 : 12
74 : 12
75 : 12
76 : 15
77 : 24
78 : 17
79 : 19
80 : 23
81 : 29
82 : 29
83 : 37
84 : 26
85 : 34
86 : 34
87 : 47
88 : 47
89 : 56
90 : 61
91 : 57
92 : 80
93 : 83
94 : 95
95 : 105
96 : 95
97 : 122
98 : 138
99 : 132
100 : 143
101 : 203
102 : 216
103 : 239
104 : 258
105 : 284
106 : 308
107 : 385
108 : 360
109 : 469
110 : 480
111 : 592
112 : 659
113 : 739
114 : 956
115 : 997
116 : 1246
117 : 1482
118 : 1776
119 : 2221
120 : 2948
121 : 4001
122 : 5686
123 : 7914
124 : 11208
125 : 15657
126 : 20329
127 : 24834
128 : 27041
129 : 26441
130 : 23124
131 : 18222
132 : 13466
133 : 9821
134 : 7095
135 : 5112
136 : 3702
137 : 2933
138 : 2207
139 : 1789
140 : 1448
141 : 1179
142 : 992
143 : 856
144 : 732
145 : 666
146 : 594
147 : 501
148 : 426
149 : 373
150 : 316
151 : 300
152 : 239
153 : 259
154 : 215
155 : 174
156 : 148
157 : 143
158 : 147
159 : 124
160 : 123
161 : 101
162 : 96
163 : 94
164 : 68
165 : 62
166 : 60
167 : 58
168 : 55
169 : 42
170 : 41
171 : 39
172 : 34
173 : 24
174 : 19
175 : 20
176 : 18
177 : 12
178 : 10
179 : 9
180 : 19
181 : 13
182 : 5
183 : 6
184 : 2
185 : 3
186 : 4
187 : 3
188 : 1
189 : 2
190 : 2
191 : 1
192 : 2
193 : 1
194 : 0
195 : 1
196 : 2
197 : 2
198 : 2
199 : 0
200 : 1
201 : 0
202 : 0
203 : 0
204 : 1
205 : 0
206 : 0
207 : 0
208 : 0
209 : 0
210 : 0
211 : 0
212 : 0
213 : 0
214 : 0
215 : 0
216 : 0
217 : 0
218 : 0
219 : 0
220 : 0
221 : 0
222 : 0
223 : 0
224 : 0
225 : 0
226 : 0
227 : 0
228 : 0
229 : 0
230 : 0
231 : 0
232 : 0
233 : 0
234 : 0
235 : 0
236 : 0
237 : 0
238 : 0
239 : 0
240 : 0
241 : 0
242 : 0
243 : 0
244 : 0
245 : 0
246 : 0
247 : 0
248 : 0
249 : 0
250 : 0
251 : 0
252 : 0
253 : 0
254 : 0
255 : 0
total : 260100
테두리 처리를 안 했기에 Total이 512*512가 나오지 않고 더 작은 값이 나온다.
문제 2 : 상관성 (Correlation) 계산
Grayscale Lenna의 상관성을 영상으로 저장해라.
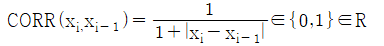
CORR=[0,1]이므로, [0, 255]를 만들기 위해서, 255를 곱해서 영상을 만들면 된다.
정답 코드
#include <iostream>
// ...
int main(void)
{
// ...
for (int i = 1; i < Height; i++) {
for (int j = 1; j < Width; j++) {
float corr = 1.0 / (1 + abs(*(YBuf + i * Width + j) - *(YBuf + i * Width + j - 1)));
corr = corr * 255;
*(Out + i * Width + j) = (BYTE)corr;
}
}
// ...
}
결과

문제 3 : JPEG 구현
전체 image가 아닌, 8x8 image block으로 실습한다.
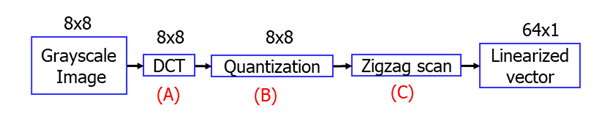
(A) FDCT (Forward DCT)
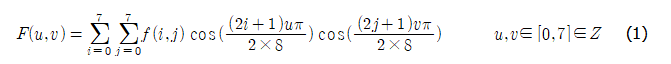
(B) F(u, v)를 양자화 (Quantization)

(C) QDCT을 zigzag scan → 1-D Linearized Vector를 만듦
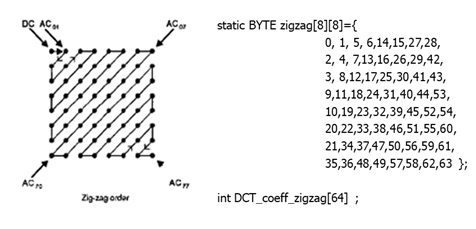
정답 코드
#include <iostream>
// ...
int main(void)
{
// ...
// 8x8 Y pixel value
BYTE fblock[8][8] = { {137, 139, 139, 136, 134, 137, 145, 152 },
{137, 137, 138, 138, 135, 136, 143, 152 },
{137, 139 ,140, 139 ,134, 144, 145, 150 },
{134, 140, 140, 138 ,140, 144, 145, 146},
{137, 139, 141 ,136 ,134, 137, 145, 140 },
{137, 139, 140, 140 ,144, 146, 144, 133},
{140, 140, 142, 146, 148, 143, 134 ,128 },
{142, 139, 139, 145, 149, 143, 132, 128 } };
// Quantization Table
static BYTE QTable[8][8] = { {16, 11, 10, 16, 24, 40, 51, 61 },
{12, 12, 14, 19, 26, 58, 60, 55 },
{14, 13 ,16, 24 ,40, 57, 69, 56 },
{14, 17, 22, 29 ,51, 87, 80, 62},
{18, 22, 37 ,56 ,68, 109, 103, 77 },
{23, 35, 55, 64 ,81, 101, 113, 92},
{49, 64, 78, 87, 103, 121, 120 ,101 },
{72, 92, 95, 98, 112, 100, 103, 99 } };
static BYTE zigzag[8][8] = {
0, 1, 5, 6,14,15,27,28,
2, 4, 7,13,16,26,29,42,
3, 8,12,17,25,30,41,43,
9,11,18,24,31,40,44,53,
10,19,23,32,39,45,52,54,
20,22,33,38,46,51,55,60,
21,34,37,47,50,56,59,61,
35,36,48,49,57,58,62,63 };
// ================= A =================
printf("\n ================= A ================= \n");
double F[8][8] = { 0.0, };
#define PI (3.14)
for (int u = 0; u < 8; u++)
{
for (int v = 0; v < 8; v++)
{
for (int i = 0; i < 8; i++)
{
for (int j = 0; j < 8; j++)
{
F[u][v] += fblock[i][j] * cos(((2 * i + 1) * u * PI) / (2 * 8)) * cos(((2 * j + 1) * v * PI) / (2 * 8));
}
}
}
}
printf("\n");
for (int u = 0; u < 8; u++)
{
for (int v = 0; v < 8; v++)
{
printf("%0.2f ", F[u][v]);
}
printf("\n");
}
// ================= B =================
printf("\n ================= B ================= \n");
int QDCT[8][8] = { 0.0, };
for (int u = 0; u < 8; u++)
{
for (int v = 0; v < 8; v++)
{
QDCT[u][v] = (int)(F[u][v] / QTable[u][v] + 0.5);
}
}
printf("\n");
for (int u = 0; u < 8; u++)
{
for (int v = 0; v < 8; v++)
{
printf("%d ", QDCT[u][v]);
}
printf("\n");
}
// ================= C =================
printf("\n ================= C ================= \n");
int DCT_coeff_zizag[64] = { 0, };
for (int u = 0; u < 8; u++)
{
for (int v = 0; v < 8; v++)
{
DCT_coeff_zizag[zigzag[u][v]] = QDCT[u][v];
}
}
for (int i = 0; i < 64; i++)
printf("%d ", DCT_coeff_zizag[i]);
printf("\n===========================================\n");
// ...
}
결과
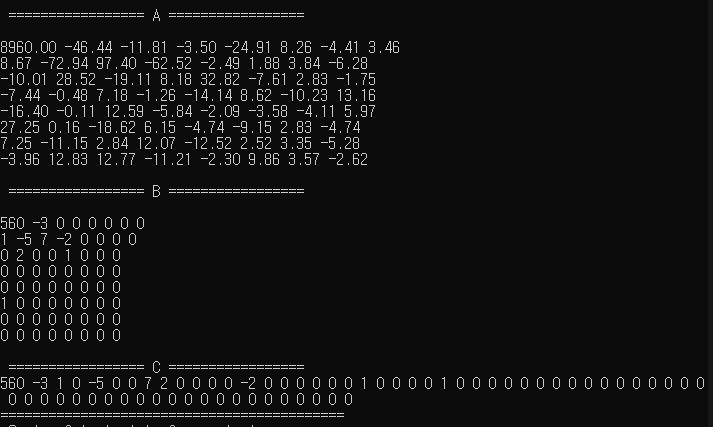
문제 4 : 엔트로피(Entropy) 계산
1. Symbol s1, s2, s3, s4의 확률 p는 각각 0.45, 0.25, 0.1, 0.2이다. Entropy H을 구하세요.
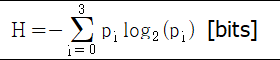
2. 확률값을 배열(array)에 저장한 후에 코딩할 것.

3. 정답 H = 1.814 bits
정답 코드
#include <iostream>
// ...
int main(void)
{
// ...
double Symbol[4] = { 0.45, 0.25, 0.1, 0.2 };
double H = 0;
for (int i = 0; i < 4; i++)
{
H += Symbol[i] * (log10(Symbol[i]) / log10(2));
}
printf(" H : %lf\n", -H);
// ...
}
결과
'공부 > 영상통신' 카테고리의 다른 글
| [영상통신] Bitwise Operation (0) | 2024.12.15 |
|---|---|
| [영상통신] 영역처리 (0) | 2024.12.15 |
| [영상통신] Pixel 처리 (0) | 2024.12.15 |


